弹跳小球模型参数说明与事件设置指南
1️⃣模型参数定义
| 参数名称 | 类型 | 默认值 | 物理意义 |
|h0 | Real | 10 | 小球初始高度(单位:米) |
|e | Real | 0.7 | 能量损耗系数(反弹后剩余速度比例) |
|g | Real | 9.8 | 重力加速度(单位:m/s²) |
2️⃣动态变量定义
| 变量名称 | 类型 | 初始值 | 物理意义 |
| h | Real | - | 小球实时高度(单位:米) |
| v | Real | 0 | 小球实时速度(单位:m/s) |
| flying | Boolean | - | 飞行状态(true=空中,false=触地) |
3️⃣核心方程与事件逻辑
1. 运动学方程
2. 飞行状态判定
flying = not (h <= 0 and v <= 0);
// 当小球高度≤0且速度≤0时判定为触地静止(flying=false)
3. 弹跳事件处理
when h <= 0 then
reinit(v, -e * pre(v)); // 触地时速度反向并按比例衰减
end when;
- 关键函数解释:
- pre(v):事件触发前瞬间的速度值。
- reinit(v, ...):重新初始化速度,实现能量损耗后的反弹。
4️⃣仿真配置建议
时间范围设置
- 开始时间:0 s
- 结束时间:15 s(可观测多次弹跳衰减过程)
5️⃣求解器配置
| 参数项 | 推荐值 | 说明 |
|------------------|-----------------|------------------------------|
| 求解器类型 | 固定步长求解器 | 适用于含事件的非连续系统 |
| 步长 | 0.01 s | 确保弹跳事件捕捉精度 |
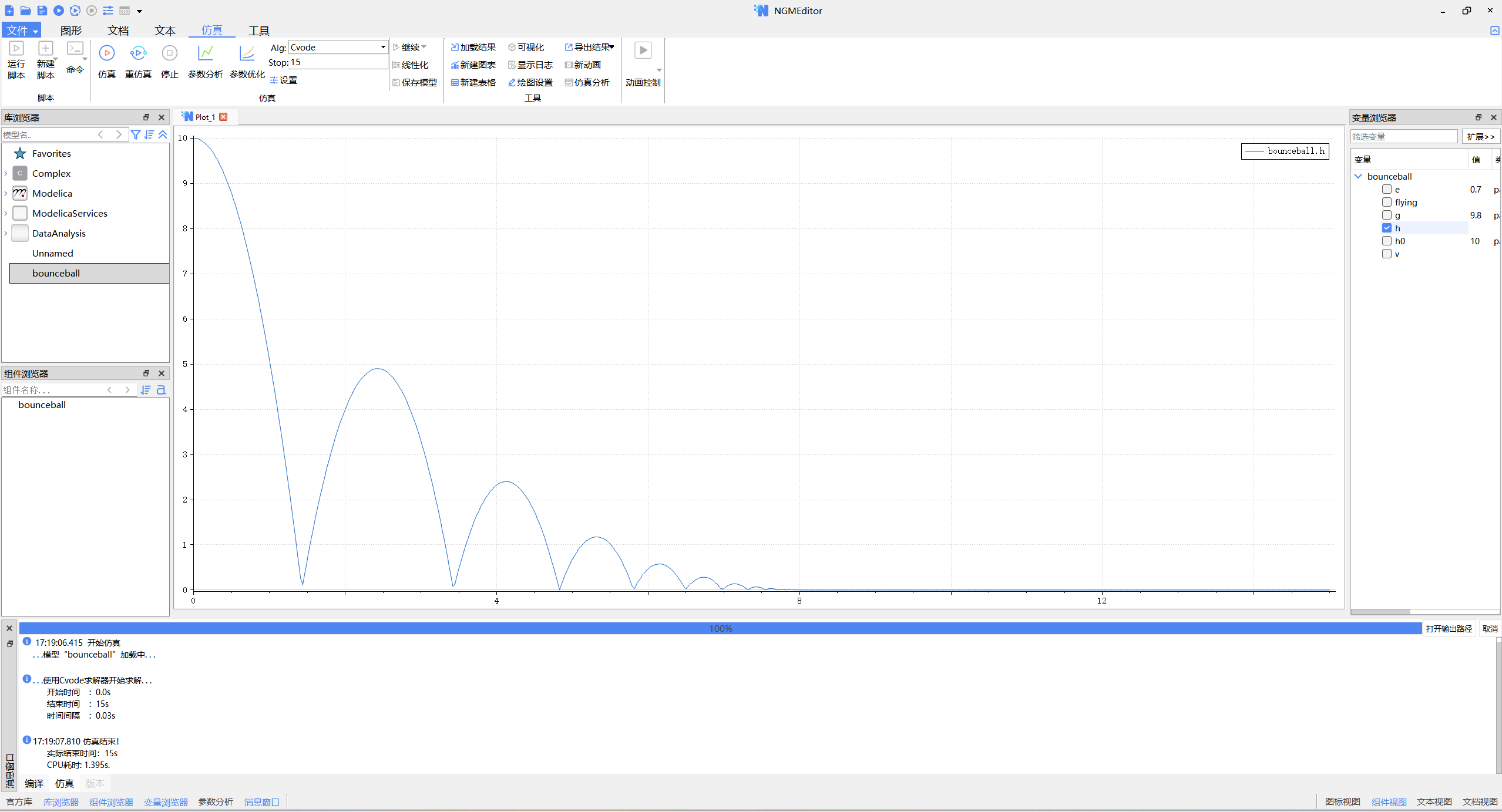
6️⃣预期仿真结果
- 高度曲线特性:
- 初始高度从 h0=10 m 开始自由下落。
- 每次触地后反弹高度按 e² 比例衰减(如第1次反弹高度为 10*0.7²=4.9 m)。
- 速度曲线特性:
- 触地瞬间速度突变为反向值(如首次触地速度由
-14 m/s 变为 9.8 m/s)。
7️⃣注意事项
- 能量守恒验证:
- 若设置 e=1(无能量损耗),系统应呈现周期性弹跳(高度不衰减)。
- 事件检测精度:
- 若步长过大可能导致触地事件延迟,建议步长≤0.01 s。
效果示意图:
- 高度曲线呈指数衰减的“锯齿波”形态,速度曲线在触地时发生突变。
模型代码:
model bounceball
parameter Real h0= 10"小球初始高度";
Real h"小球高度";
Real v(start = 0)"小球速度";
parameter Real e=0.7"能量损耗剩余比例";
Boolean flying"小球飞行状态";
parameter Real g= 9.8"重力加速度";
initial equation //初始化状态方程
h = h0;
v = 0;
equation
der(h) = v;
der(v) = if flying then -g else 0;//如果飞行中没有触地,受重力,加速度g方向向下,触地后重力支持力平衡
flying = not ( h <= 0 and v <= 0);//判断是否在下落过程中
when h <= 0 then
reinit( v, -e * pre(v));//触地后触发反弹事件
end when;
end bounceball;