参数说明:
parameter Real h0= 10 "小球初始高度";
parameter Real e=0.7 "能量损耗剩余比例";
parameter Real g= 9.8 "重力加速度";
变量说明:
Real h "小球高度";
Real v(start = 0) "小球速度";
Boolean flying "小球飞行状态";
方程和事件部分:
der(h) = v;:这是一个微分方程,表明小球高度 h 的导数等于其速度 v,即高度随时间的变化率就是速度。
der(v) = if flying then -g else 0;:这是一个条件微分方程。如果小球处于飞行状态(flying 为 true),则小球的加速度为 -g(负号表示重力方向向下);如果小球不处于飞行状态(触地静止),则加速度为 0。
flying = not ( h <= 0 and v <= 0);:该方程用于判断小球是否处于飞行状态。当小球高度 h 小于等于 0 且速度 v 小于等于 0 时,认为小球触地静止,flying 为 false;否则,flying 为 true。
when h <= 0 then ... end when;:这是一个事件触发结构,当小球高度 h 小于等于 0 时,触发事件。
reinit( v, -e * pre(v));:reinit 函数用于重新初始化变量的值。pre(v) 表示事件触发前 v 的值,这里将小球触地后的速度重新初始化为反弹前速度的 -e 倍,负号表示速度方向反转,e 表示能量损耗。
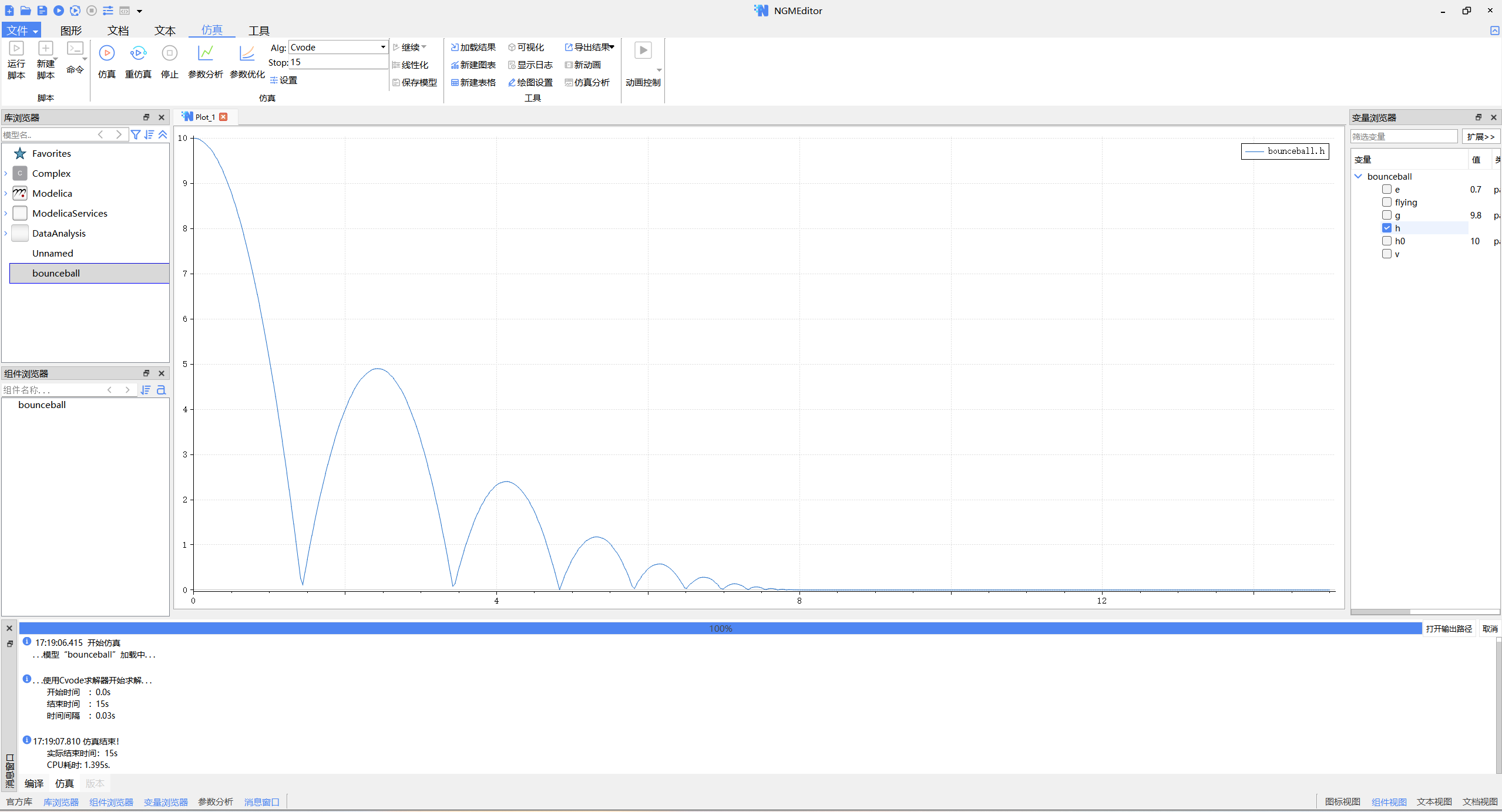
仿真事件推荐设置开始事件0s 结束时间15s
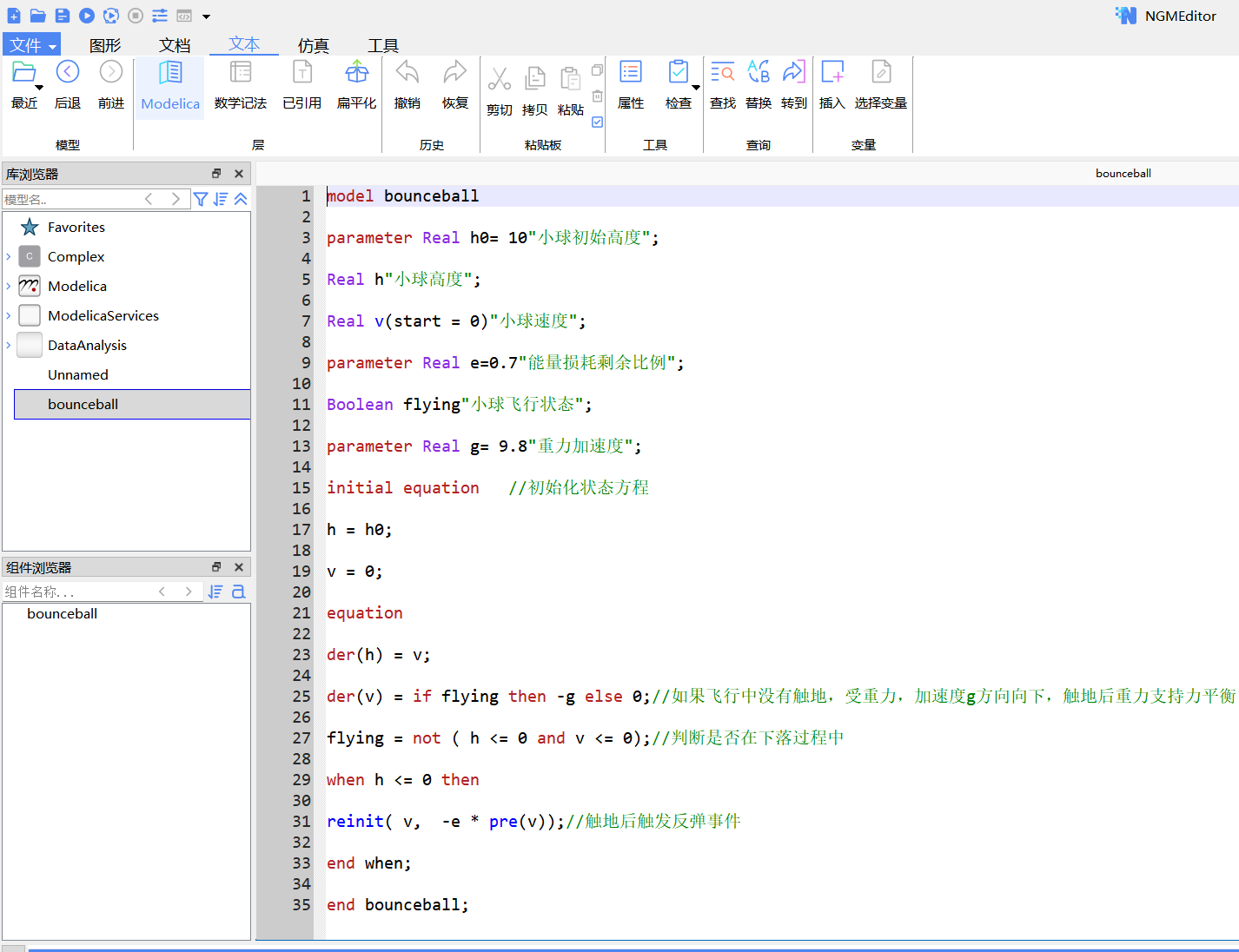
模型代码:
model bounceball
parameter Real h0= 10"小球初始高度";
Real h"小球高度";
Real v(start = 0)"小球速度";
parameter Real e=0.7"能量损耗剩余比例";
Boolean flying"小球飞行状态";
parameter Real g= 9.8"重力加速度";
initial equation //初始化状态方程
h = h0;
v = 0;
equation
der(h) = v;
der(v) = if flying then -g else 0;//如果飞行中没有触地,受重力,加速度g方向向下,触地后重力支持力平衡
flying = not ( h <= 0 and v <= 0);//判断是否在下落过程中
when h <= 0 then
reinit( v, -e * pre(v));//触地后触发反弹事件
end when;
end bounceball;