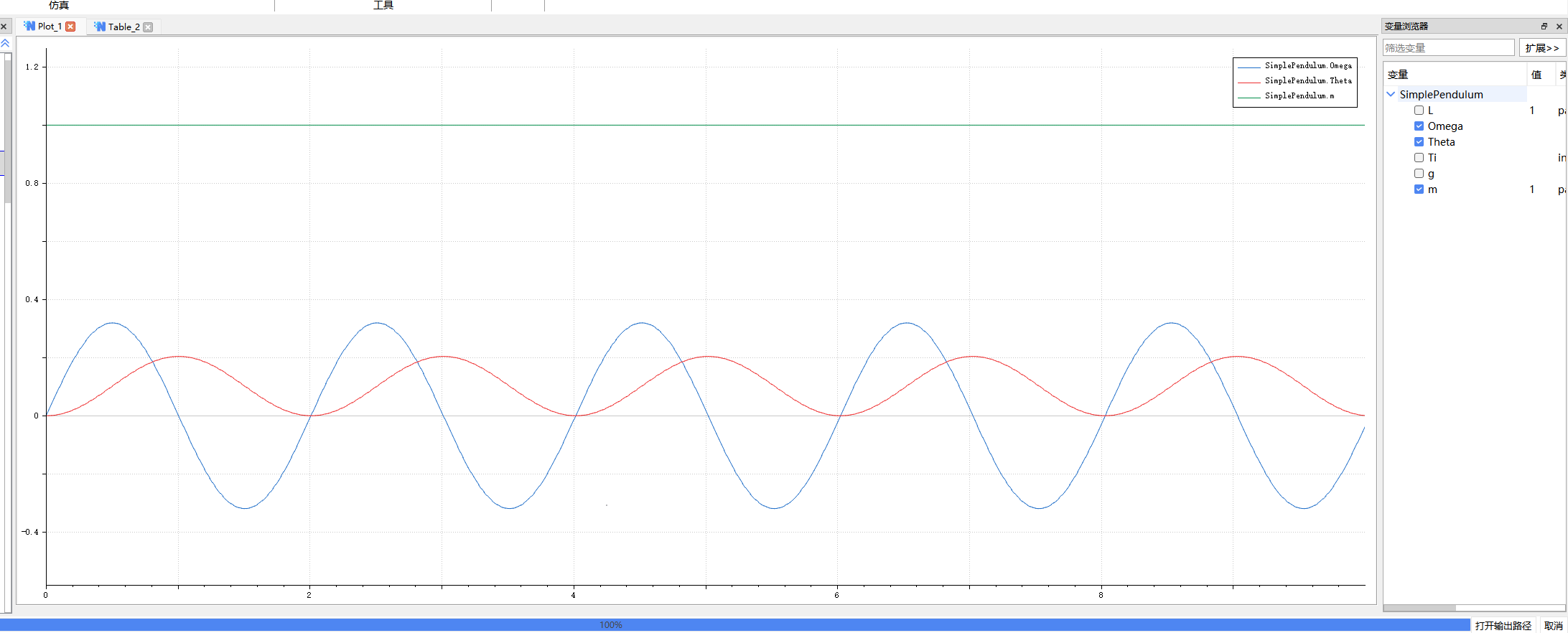
这里的SimplePendulum模型描述了一个在重力作用下的摆动系统,其中:
g 是重力加速度(9.8 m/s²),
m 是摆的质量(1 kg),
L 是摆的长度(1 m),
Ti 是输入的控制信号(一个实数输入,初始化为 1),
Θ 是摆角度(单位是弧度),
Ω 是摆的角速度。
代码解析:
modelica
Copy
Edit
model SimplePendulum
constant Real g=9.8; // 重力加速度
parameter Real m=1; // 摆的质量
parameter Real L=1; // 摆的长度
input Real Ti(start=1); // 控制输入信号
Real Theta(start=0); // 摆的角度
Real Omega; // 摆的角速度
equation
Omega = der(Theta); // 摆角度的导数是角速度
der(Omega) + gTheta/L = Ti/(mL2); // 摆的运动方程:角加速度与控制信号和摆的状态相关
end SimplePendulum;
解释:
常量和参数:
g=9.8 是标准的地球重力加速度(单位 m/s²)。
m=1 是摆的质量(单位 kg)。
L=1 是摆的长度(单位 m)。
变量:
Theta 是摆的角度(单位是弧度),并且在仿真开始时被初始化为0。
Omega 是摆的角速度(单位是弧度/秒)。
运行时:
Ti 控制输入信号在仿真中设置为1,并可以根据实际需要进行更改。
Theta 是初始角度(0弧度),随着仿真进程会发生变化。
Omega 是角速度,随着仿真时间变化。